Differentiable Simulators

Differentiable Simulators

While Deep Learning models have had temendous success at learning compex functions, they are highly sensitive to distribution shifts, and further require tremendous amounts of data to learn. When the functions being learned involve physical processs, one can sometimes remove the need for learning and instead rely on physics laws that simulate the process. Such laws can be Netwon’s laws of mechanics for estimating the movements of planets or of particles in statistical physics, Maxwell’s equations for electromagnetism, or the Navier-Stokes equations in fluid dynamics.

In the case of MRI scans, one can simulate the Bloch differential equation which describes the evolution of magnetization of an MRI voxel over time:

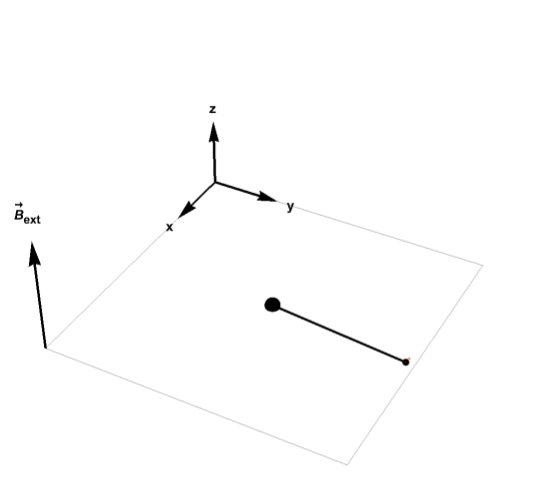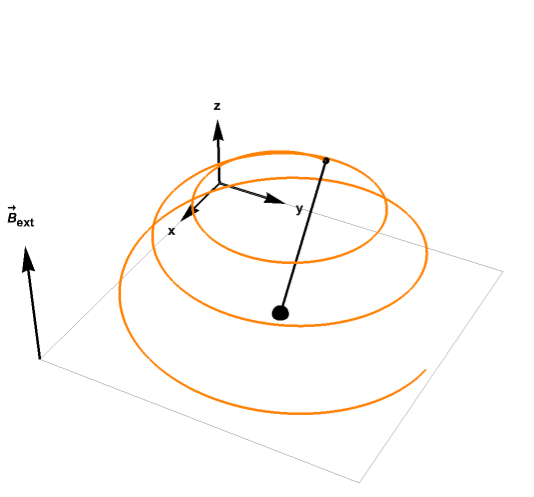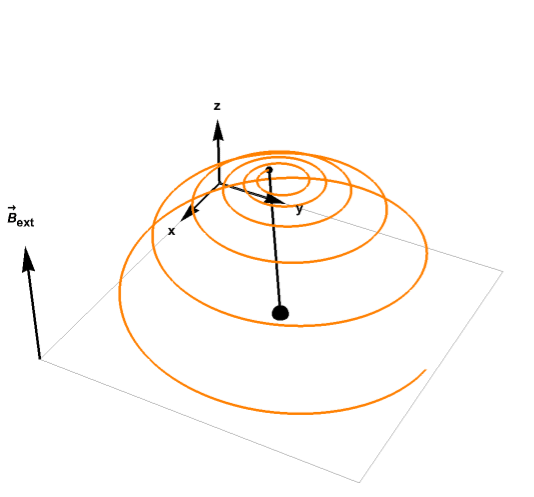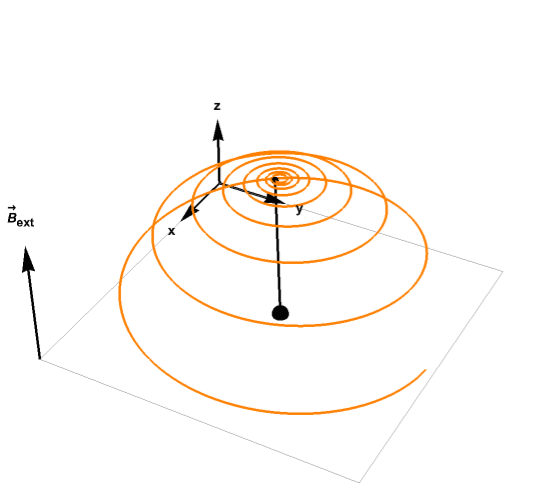
alt text

For example, the plot below shows how the magnetization vector relaxes to equilibrium while precessing around the magnetic field:

alt text

While integrating the Bloch equation can be computationally intensive for a long MRI sequence, a faster method uses the Extended Phase Graph method, which projects the signal into the Fourier basis and simulates the MRI sequence in the Fourier space directly. Since an MRI sequence contains a combination of radiofrequency (RF) pulses, gradients and free precession, this method can estimate how each of these components change the coefficients of the Fourrier basis.

While many such simulators exist for MRI, until recently no such simulators were differentiable. Diffentiability allows one to very efficiently optimize the input parameters (image phantom and MRI sequence) to match a desired signal. Through differentiability, we are essentially using the deep-learning machinery to perform optimizations, and to

The main aim of this line of work is to implement such simulators for MRI (+diffusion MRI, PET or CT) in a deep learning framework (e.g. PyTorch), in order to enable the use of automatic differentiation and backpropagation. For a given target image, this would enable us to optimize using Stochastic Gradient Descent the parameters of the simulator, or even the input brain phantom.

Diffusion MRI

Diffusion MRI is a type of MRI which can be used to infer tissue microstructure (morphology of cells, packing density, orientation of neuronal axons, etc …). It works by measuring the diffusion of water molecules, which is restricted by the cell and tissue compartments:

See below a short video on how diffusion MRI works:


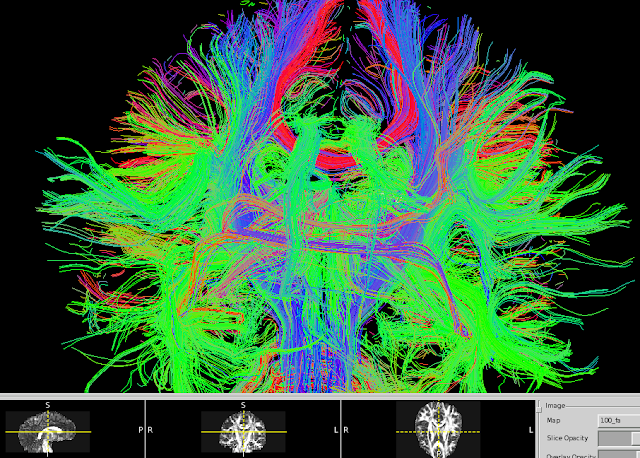
In particular, diffusion MRI enables us to get these incredible images of white matter tracts in the brain:

alt text

We are working on a differentiable simulator for Diffusion MRI. For simulating diffusion MRI, an additional diffusion term is added to the Bloch equation, thus making the Bloch-Torrey equation:

A diffusion MRI simulator called SpinDoctor has been proposed by Li et al, which solve the diffusion equation either through numerical integration, or using a matrix formalism. We are currently working on re-implementing SpinDoctor in PyTorch in order to make it differentiable, and then perform gradient-based optimization of the 3D input meshes based on a given MRI signal.

Additional materials on MRI:

Further reading on Diffusion MRI:

Avatar
Razvan Marinescu
Assistant Professor

My research interests are in Machine Learning, and it’s applications in Healthcare and Molecular Biology. I am doing research in generative models, bayesian modelling, causal ML, compositional ML and multimodal modelling.